Question

Evaluate i^i. Is this real, imaginary or neither?

Answer 1

The number
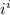`i^i` is a real number.

Explanation:

First, let us recall the exponential form of a complex number: if
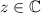`z\in\mathbb{C}` it can be written as

`z=re^(i\phi)`

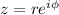
where
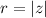`r=|z|` and
`\phi` is the argument of
`z`.

Also, let us recall Euler's formula: if x is a real number

`e^(ix) = \cos x +i\sin x`.

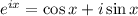Using this, we have

`e^(i\pi/2) = \cos(\pi)/(2) + i\sin(\pi)/(2) = i`.

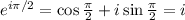So, if we elevate both sides to
`i`

`\left(e^(i\pi/2)\right)^i = i^i`.

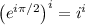But,
`\left(e^(i\pi/2)\right)^i = e^(i^2\pi/2) = e^(-\pi/2)`.

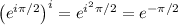Therefore,
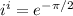`i^i = e^(-\pi/2)` which is a real number.