Question

Determine a polynomial function whose graph passes through the given points. 5: (0,-5); (1,-4) ; (-1,-9); (2,-3),

Answer 1

The interpolating polynomial is

`p(x) = (1)/(2)x^3-(3)/(2)+2x-5`.

Explanation:

First, notice that we want to calculate the interpolating polynomial through the points (0,-5); (1,-4) ; (-1,-9); (2,-3). This means that we want to find a polynomial
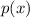`p(x)` such that

`p(-1) = -9`,
`p(0) = -5`
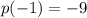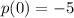
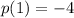`p(1) = -4` and
`p(2) = -3`.

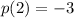We will have four equations, so our polynomial will be, at most, of degree 3. Let us write

`p(x) = a_0 + a_1x +a_2x^2 +a_3x^3.`

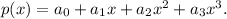
The coordinates give us the following equations:

`\begin{cases} -9= p(-1) &= a_0 - a_1 +a_2 -a_3 \\ -5=p(0) &= a_0 \\-4=p(1) &= a_0 + a_1 +a_2 +a_3 \\ -3 = p(2) &= a_0 + 2a_1 +4a_2 +8a_3 \end{cases}`

Notice that from the second equation we know that
`a_0 =-5`. Then, we obtained the linear system of equations

`\begin{cases} -9 &= -5 - a_1 +a_2 -a_3 \\-4 &= -5 + a_1 +a_2 +a_3 \\ -3 &= -5 + 2a_1 +4a_2 +8a_3 \end{cases}`

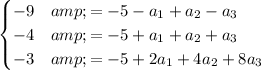
which is equivalent to

`\begin{cases} - a_1 +a_2 -a_3 &= -4\\ a_1 +a_2 +a_3 &= 1\\ 2a_1 +4a_2 +8a_3 &= 2\end{cases}`.

So, we have reduced our interpolation problem to solve a linear system of equations. Now, notice that if we add the first two equations of the system we obtain

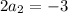`2a_2=-3` that yields
`a_2 = -(3)/(2)`.

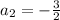Then, our system becomes

`\begin{cases}-a_1 -(3)/(2)-a_3 &= -4\\a_1 -(3)/(2) +a_3 &= 1\\ 2a_1 -6 +8a_3 &= 2\end{cases}`

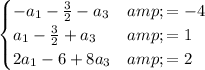
which is equivalent to

`\begin{cases}-a_1-a_3 &=-(5)/(2)\\a_1+a_3 &=(5)/(2)\\ 2a_1+8a_3 &=8\end{cases}`.

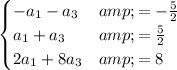Recall that now the first two equations are just the same, so we will use the first and third ones:

`\begin{cases}-a_1-a_3 &=-(5)/(2)\\2a_1+8a_3 &= 8\end{cases}`.

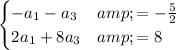If we multiply the first one and add it to the second we get:

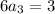`6a_3 = 3` that yields
`a_3 = (1)/(2)`.

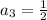Thus, substituting this value in the first equation:

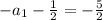`-a_1-(1)/(2) = -(5)/(2)` which is equivalent to
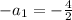`-a_1=-(4)/(2)`. Then,
`a_1=2`.

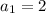Summing up all our results we get that the interpolating polynomial is

`p(x) = (1)/(2)x^3-(3)/(2)+2x-5`.