Question

A cable hangs between a street pole and a house that are 3 m apart. The height of the cable above the ground is approximated by the function f(x) = cosh(x) + 3, with the lowest point 1 m from the house and 2 m from the pole. Use the arc length integral to compute the length of the chain. You do not have to use the Riemann sum approach to construct the integral formula; just use it.

Answer 1

The arc length integral takes complex values.

Explanation:

This function
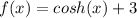`f(x) = cosh(x) + 3` has a minimun in
`x=0`.

Then we can estimate that the pole is 2 m at the left of
`x=0`, in
`x=-2`, and the house, 1 m at the rigth:
`x=1`.

The arc length we have to calculate goes from
`x=-2` to
`x=1`

The arc length integral equation is:

`S=\int\limits^a_b {√(1+f'(x)) \, dx`

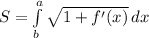
that is derived from the Riemann's sum

`S=\sum\limits^n_(i=1) {√(1+\Delta y_i/\Delta x_i) \, \Delta x_i`

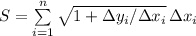
To compute
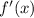`f'(x)` we derive
`f(x) = cosh(x) + 3` :

`f'(x)=(d(cosh(x))/(dx) +(d(3))/(dx)=sinh(x)`

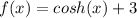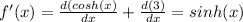
The function
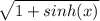`\sqrt{1+sinh(x)` in the range of x between x=-1 to x=0 takes complex values that prevent calculating the sum or the integral within the scope of the real values.