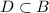Answer:
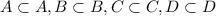 ,
,
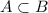 ,
,
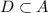 and
and
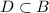 .
.
Explanation:
The given sets are
A={n ∈ P:n is odd}
B = {n ∈ P:n is prime)
C = {4n +3:n ∈ P}
D = {x ∈ R : x² - 8x + 15 = 0}
P is the set of prime numbers and R is the set of real numbers.



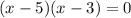
So, the elements of all sets are
A = {3, 5, 7, 11, 13, 17, 19, 23, ...}
B = {2, 3, 5 , 7, 11, 13, 17, 19, 23, ...}
C = {11, 15, 23, ...}
D = {3,5}
Each sets is a subset of it self. So,
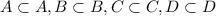
All the elements of A lie in set B, so A is a subset of B.
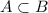
Since
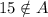 and
and
 , So, C is not the subset of A and B.
, So, C is not the subset of A and B.
D has two elements, 3 and 5, Since
 and
and
 , therefore
, therefore
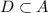 and
and