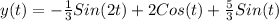Answer:
The solution of the differential equation is
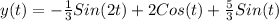
Explanation:
The differential equation is given by: y" + y = Sin(2t)
i) Using characteristic equation:
The characteristic equation method assumes that y(t)=
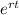 , where "r" is a constant.
, where "r" is a constant.
We find the solution of the homogeneus differential equation:
y" + y = 0

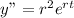
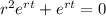

As
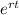 could never be zero, the term (r²+1) must be zero:
could never be zero, the term (r²+1) must be zero:
(r²+1)=0
r=±i
The solution of the homogeneus differential equation is:
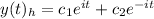
Using Euler's formula:
![y(t)_(h)=c_(1)[Sin(t)+iCos(t)]+c_(2)[Sin(t)-iCos(t)]](https://img.qammunity.org/2020/formulas/mathematics/college/jjsoufltxb6m3af7famctm7wuxlyzd2e47.png)
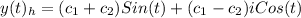
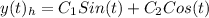
The particular solution of the differential equation is given by:



So we use these derivatives in the differential equation:
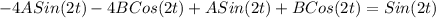

As there is not a term for Cos(2t), B is equal to 0.
So the value A=-1/3
The solution is the sum of the particular function and the homogeneous function:

Using the initial conditions we can check that C1=5/3 and C2=2
ii) Using Laplace Transform:
To solve the differential equation we use the Laplace transformation in both members:
ℒ[y" + y]=ℒ[Sin(2t)]
ℒ[y"]+ℒ[y]=ℒ[Sin(2t)]
By using the Table of Laplace Transform we get:
ℒ[y"]=s²·ℒ[y]-s·y(0)-y'(0)=s²·Y(s) -2s-1
ℒ[y]=Y(s)
ℒ[Sin(2t)]=
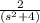
We replace the previous data in the equation:
s²·Y(s) -2s-1+Y(s) =
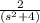
(s²+1)·Y(s)-2s-1=
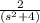
(s²+1)·Y(s)=

Y(s)=
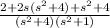
Y(s)=
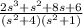
Using partial franction method:
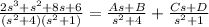
2s^{3}+s^{2}+8s+6=(As+B)(s²+1)+(Cs+D)(s²+4)
2s^{3}+s^{2}+8s+6=s³(A+C)+s²(B+D)+s(A+4C)+(B+4D)
We solve the equation system:
A+C=2
B+D=1
A+4C=8
B+4D=6
The solutions are:
A=0 ; B= -2/3 ; C=2 ; D=5/3
So,
Y(s)=
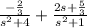
Y(s)=
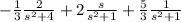
By using the inverse of the Laplace transform:
ℒ⁻¹[Y(s)]=ℒ⁻¹[
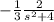 ]-ℒ⁻¹[
]-ℒ⁻¹[
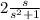 ]+ℒ⁻¹[
]+ℒ⁻¹[
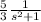 ]
]