Question

Convert the following expression to CNF (Conjunctive Normal Form) format using the propositional laws:

(p → q) → r

In your answer make sure that you (1) Show your steps (2) Do not skip any steps and (3) Justify each step with the name of the law being used.

Part(b) [50 points].

(i)(25 points) Prove that the Method of Affirming (Modus Ponens) is sound using truth tables.

(ii)(25 points) Prove that the Method of Denying (ModusTollens) is sound using truth tables.

Answer 1

See steps below

Explanation:

a)

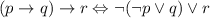`(p\rightarrow q)\rightarrow r\Leftrightarrow \\eg(\\eg p\vee q)\vee r` equivalence of (r implies s) with (not r or s)

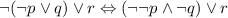`\\eg(\\eg p\vee q)\vee r\Leftrightarrow (\\eg \\eg p\wedge \\eg q)\vee r` De Morgan's Law

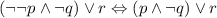`(\\eg \\eg p\wedge \\eg q)\vee r\Leftrightarrow (p\wedge \\eg q)\vee r` Double negation

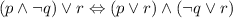`(p\wedge \\eg q)\vee r\Leftrightarrow (p\vee r)\wedge (\\eg q\vee r)` Distributive Law

The last expression is in CNF.

b)

i)

Modus Ponens states the following,

If (p implies q) is true and p is true, then q is true.

By watching the truth table of implication

`\left[\begin{array}{ccc}p&q&p\rightarrow q\\T&T&T\\T&F&F\\F&T&T\\F&F&T\end{array}\right]`

We can notice that the only row that satisfies

(p implies q) is true and p is true

is the first row, so q must be true.

ii)

Modus Tollens states that if (p implies q) is true and (not q) is true, then (not p) is true.

By watching the following truth table

`\left[\begin{array}{ccccc}p&q&\\eg p&\\eg q&p\rightarrow q\\T&T&F&F&T\\T&F&F&T&F\\F&T&T&F&T\\F&F&T&T&T\end{array}\right]`

We can notice that the only row that satisfies (p implies q) is true and (not q) is true, is the fourth row, so (not p) must be true.