Question

Will ran the diagonal distance across a square field measuring 40 yards on each side. James ran the diagonal distance across a rectangular field with a length if 25 yards and a width of 35 yards. Who ran a longer distance? Show work to prove your answer.

Answer 1

Answer: The distance across a rectangular field is longer distance.

Explanation:

Since we have given that

Dimension of square = 40 yards

So, Dimensions of rectangle are :

Length = 25 yards

Width = 35 yards

So, Perimeter of rectangle would be

`2* (l+b)\\\\=2* (25+35)\\\\=2* 60\\\\=120\ yards`

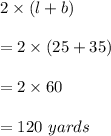
Diagonal of square would be

`√(40^2+40^2)\\\\=√(1600+1600)\\\\=√(3200)\\\\=56.56\ yards`

Hence, the distance across a rectangular field is longer distance.

Answer 2

Will ran the longer distance.

Explanation:

In order to calculate this you have to create a triangle with the values that you are given, and the distance ran would be the hypothenuse, remember the formula for hypothnuse:

`H=\sqrt[2]{a^2+b^2}`

Now we just insert the values into the formula:

`H=\sqrt[2]{a^2+b^2}\\H=\sqrt[2]{40^2+40^2}\\H=56,56`

`H=\sqrt[2]{a^2+b^2}\\H=\sqrt[2]{25^2+35^2}\\H=43,01`

AS you can see the hypothenuse in the square is greater than that of the rectangle, so Will who ran the hypothenuse of the square will be the one that ran the longer distance.