Answer:
The correct answer is E.
Explanation:
First I look for the relationships between the coefficients. The first term corresponds to the base value.
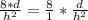
The second term corresponds to the value obtained when the density of the underlying material is doubled and the daily usage of the equipment is halved.
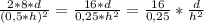
With the I get the ratio of coefficients of
 :
:
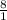 = 8
= 8
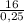 = 64
= 64
Now I calculate the percentage increase in the useful life of the equipment as:
% =
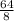 * %100 = %800
* %100 = %800