Question

Calculate the pressure exerted by Ar for a molar volume of 1.31 L mol–1 at 426 K using the van der Waals equation of state. The van der Waals parameters a and b for Ar are 1.355 bar dm6 mol–2 and 0.0320 dm3 mol–1, respectively. Is the attractive or repulsive portion of the potential dominant under these conditions?

Answer 1

Attractive

Step-by-step explanation:

Given that:

Temperature = 426 K

Volume / moles = 1.31 L / mol

So, for n = 1 , V = 1.31 L

Using ideal gas equation as:

PV=nRT

where,

P is the pressure

V is the volume

n is the number of moles

T is the temperature

R is Gas constant having value = 0.08314 L bar/ K mol

Applying the equation as:

P × 1.31 L = 1 × 0.08314 L bar/ K mol × 426 K

⇒P (ideal) = 27.0363 bar

Using Van der Waal's equation

`\left(P+(an^2)/(V^2)\right)\left(V-nb\right)=nRT`

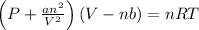
R = 0.08314 L bar/ K mol

Where, a and b are constants.

1 L = 1 dm³

For Ar, given that:

So, a = 1.355 bar dm⁶ / mol² = 1.355 bar L² / mol²

b = 0.0320 dm³ / mol = 0.0320 L / mol

So,

`\left(x+(1.355* \:1^2)/(1.31^2)\right)\left(1.31-0.032\right)=35.41764`

`(\left(x+(1.355* \:1^2)/(1.31^2)\right)\left(1.31-0.032\right))/(1.278)=(35.41764)/(1.278)`

`x+(1.355)/(1.7161)=(35.41764)/(1.278)`

`x=(59.04852)/(2.1931758)`

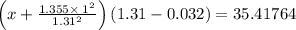
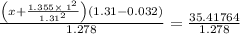
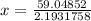
⇒P (real) = 26.9238 bar

Thus, P (real) is smaller than P (ideal) , the attractive force will dominate.