Answer:
The probability that no one sits in the same seat on both days of that week is given by,

Explanation:
Given : A certain class has 20 students, and meets on Mondays and Wednesdays in a classroom with exactly 20 seats. In a certain week, everyone in the class attend both days. On both days, the students choose their seats completely randomly (with one student per seat).
To find : The probability that no one sits in the same seat on both days of that week ?
Solution :
Let
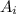 be the i-th student sits on seat which he has been sitting on Monday.
be the i-th student sits on seat which he has been sitting on Monday.
According to question,
We have to calculate
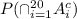
Applying inclusion exclusion formula,
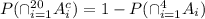
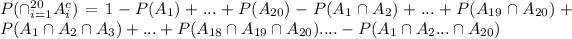
Using symmetry,
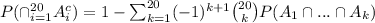
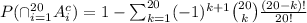
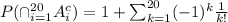
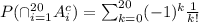

Therefore, The probability that no one sits in the same seat on both days of that week is given by,
