Question

An instructor in a large lecture class found, at the end of the semester, that the total point distribution in his class was approximately Normal, with a mean of 530 and a standard deviation of 80. If 10% of the class is to receive A’s (the instructor grades on a curve), what is the lowest number of points that a student can have and still earn an A?

Answer 1

Answer: The lowest number of points that a student can have and still earn an A is 632.

Explanation:

Since we have given that

Mean = 530

Standard deviation = 80

If 10% of the class is to receive A's, then we need to find the lowest number of points that a student can have and still earn an A.

Let X be the number of points.

so,
`P(X\geq x)=0.10`

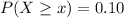
so, it becomes,

`P((X-\mu)/(\sigma)\geq (x-530)/(80))=0.10\\\\P(Z\geq (x-530)/(80))=0.10\\\\P(Z\leq (x-530)/(80))=1-0.10=0.90`

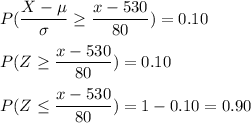
From the Z-table, we get that

`P(Z\leq 1.28)=0.90`

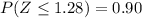
So, we get that

`(x-530)/(80)=1.28\\\\x-530=1.28* 80\\\\x-530=102.4\\\\x=102.4+530\\\\x=632.4`

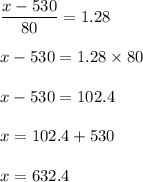
Hence, the lowest number of points that a student can have and still earn an A is 632.