Answer:
Proved
Explanation:
Let a, b be two odd numbers
We know odd numbers give remainder as 1 when divided by 2
Hence a and b can be written as
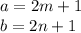 , for some integers m and n.
, for some integers m and n.
Now product
=
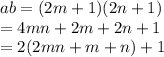
We have when m and n are integers, 2mn+m+n also will be an integer say s
Then product
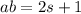
again gives remainder 1 when divided by 2
Hence product is odd.