Question

The sum of the first n positive odd numbers is square.

Answer 1

See explanation below

Explanation:

All the odd numbers can be written as 2n-1 where n is an integer.

The sum (S) of the first n positive odd numbers can be written as:

`S=1+3+5+.........+(2n-5)+(2n-3)+(2n-1)`

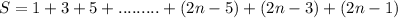
If we change the order to a decreasing order we would write it this way:

`S=(2n-1)+(2n-3)+(2n-5)+.........+5+3+1`

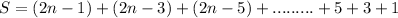
Let's sum up both equations, we are going to pair the first number of our first equation with the first number of our second equation, we can see that each pair sums up 2n ( let's see this: (2n-1 + 1 =2n, 2n-3 + 3 = 2n, 2n-5 + 5 = 2n...)) therefore we would get n pairs that sum up 2n.

`2S=n(2n)\\2S=2n^(2) \\S=n^(2)`

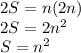
Therefore, the sum of the first n positive odd numbers is square.