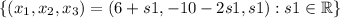Question

Find all solutions by transforming the system to reduced echelon form and back substituting. (If there are an infinite number of solutions use s1 as your parameter. If there is no solution, enter NO SOLUTION.)

2x1 + x2 = 2

−x1 − x2 − x3 = 4

Answer 1

The system has infinite solutions described in the set
`\{(x_1,x_2,x_3)=(6+s1, -10-2s1,s1): s1\in\mathbb{R}\}`

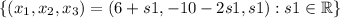
Explanation:

The augmented matrix of the system is
`\left[\begin{array}{cccc}-1&-1&-1&4\\2&1&0&2\end{array}\right]`.

We apply row operations:

1. We add the first row to the second row twice and obtain the matrix
`\left[\begin{array}{cccc}-1&-1&-1&4\\0&-1&-2&10\end{array}\right]`

2. multiply by -1 the rows of the previous matrix and obtain the matrix
`\left[\begin{array}{cccc}1&1&1&-4\\0&1&2&-10\end{array}\right]` that is the reduced echelon form of the matrix associated to the system.

Now we aply backward substitution:

1. Observe that the reduced echelon form has a free variable, then the system has infinite solutions.

2.

`x_2+2x_3=-10\\x_2=-10-2x_3`

3.

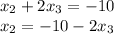
`x_1+x_2+x_3=-4\\x_1-10-2x_3+x_3=-4\\x_1-x_3=-4+10\\x_1=6+x_3`.

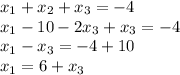Then the set of solutions is
`\{(x_1,x_2,x_3)=(6+s1, -10-2s1,s1): s1\in\mathbb{R}\}`