Question

A block of mass m = 1.00 kg is attached to a spring of force constant k = 500 N/m. The block is pulled to a position xi= 5.00 cm to the right of equilibrium and released from rest. Find the speed the block has as it passes through equilibrium if the coefficient of friction between block and surface is 0.350.

Answer 1

The speed of the block is 4.96 m/s.

Step-by-step explanation:

Given that.

Mass of block = 1.00 kg

Spring constant = 500 N/m

Position
`x_(i)=5.00\ cm`

Coefficient of friction = 0.350

(A). We need to calculate the speed the block has as it passes through equilibrium if the horizontal surface is friction less

Using formula of kinetic energy and potential energy

`(1)/(2)mv^2=(1)/(2)kx^2-\mu mgx`

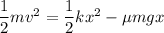
Put the value into the formula

`(1)/(2)*1.00* v^2=(1)/(2)*500*(5.00*10^(-2))-0.350*1.00*9.8*5.00*10^(-2)`

`v^2=(2*12.3285)/(1.00)`

`v^2=24.657`

`v=4.96\ m/s`

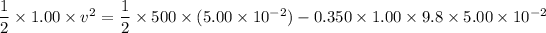
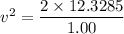
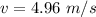
Hence, The speed of the block is 4.96 m/s.