Are there concepts/processes to strictly follow in writing radicals as expressions with rational exponents?

Question

asked Jul 20, 2022 98.9k views

1 Answer

Ofir Fridman · Answer 1 · 2022-07-27T01:36:13+0000

Answer:

The concept or process is
$x^{(m)/(n)}=(\sqrt[n]{x})^m$ .

Explanation:

Consider the provided information.

The following property can be used to rewrite each radical as an exponent.

The numerator tells the power of the resulting rational exponent, and the denominator of the rational exponents tells the root of that number.

$x^{(m)/(n)}=(\sqrt[n]{x})^m$

For example:

$(27)^{(2)/(3)}=(\sqrt[3]{27})^2$

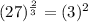
$(27)^{(2)/(3)}=(3)^2$

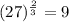
$(27)^{(2)/(3)}=9$

Hence, the concept or process is
$x^{(m)/(n)}=(\sqrt[n]{x})^m$ .