Question

Consider the function on the interval (0, 2π). f(x) = 7 sin2(x) + 7 sin(x) (a) Find the open interval(s) on which the function is increasing or decreasing. (Enter your answers using interval notation.) increasing decreasing (b) Apply the First Derivative Test to identify all relative extrema. relative maxima (x, y) = (smaller x-value) (x, y) = (larger x-value) relative minima (x, y) = (smaller x-value) (x, y) = (larger x-value)

Answer 1

Answer with Step-by-step explanation:

Given

`f(x)=7sin(2x)+7sin(x)`

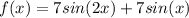
Differentiating both sides by 'x' we get

`14cos(2x)+7cos(x)=f'(x)`

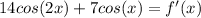
Now we know that for an increasing function we have

`f'(x)>0\\\\14cos(2x)+7cos(x)>0\\\\2cos(2x)+cos(x)>0\\\\2(2cos^(2)(x)-1)+cos(x)>0\\\\4cos^(2)(x)+cos(x)-2>0\\\\(2cos(x)+(1)/(2))^2-2-(1)/(4)>0\\\\(2cos(x)+(1)/(2))^2>(9)/(4)\\\\2cos(x)>(3)/(2)-(1)/(2)\\\\\therefore cos(x)>(1)/(4)\\\\\therefore x=[0,cos^(-1)(1/4)]\cup [2\pi-cos^(-1)(1/4),2\pi ]`

Similarly for decreasing function we have

`[tex]f'(x)<0\\\\\therefore cos(x)<1/4\\\\x<cos^(-1)((1)/(4))\\\\x=[cos^(-1)((1)/(4)),2\pi -cos^(-1)((1)/(4))]`

Part b)

To find the extreme points we equate the derivative with 0

`f'(x)=0\\\\cos(x)=(1)/(4)\\\\x=cos^(-1)((1)/(4))`

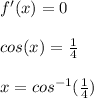
Thus point of extrema is only 1.