Question

A publisher reports that 35% of their readers own a particular make of car. A marketing executive wants to test the claim that the percentage is actually less than the reported percentage. A random sample of 140 found that 25% of the readers owned a particular make of car. Is there sufficient evidence at the 0.02 level to support the executive's claim?

Answer 1

There is sufficient evidence to support the executive's claim.

Explanation:

We will do a two-tailed test of the proportion.

Null hypothesis H0: p=0.35

Alternative hypothesis: p≠0.35

The significance level is 0.02.

Calculation of the standard deviation

`\sigma=\sqrt{(p*(1-p))/(n) }=\sqrt{(0.35*(1-0.35))/(140)} =0.04`

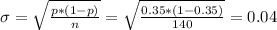
Calculation of the z-score

`z=(p-P)/\sigma=(0.25-0.35)/0.04=-2.5`

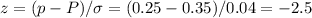
Since we have a two-tailed test, the P-value is the probability that the z-score is less than -2.5 or greater than 2.5.

Calculation of the P-value

`P=P(x<-2.5)+P(x>2.5)=0.00621+0.00621=0.01242`

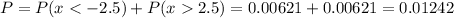
Since the P-value (0.012) is smaller than the significance level (0.02), we can reject the null hypothesis.

There is sufficient evidence to support the executive's claim.