Question

An optical inspection system is used to distinguish among different part types. The probability of a correct classification of any part is 0.96. Suppose that three parts are inspected and that the classifications are independent. Let the random variable X denote the number of parts that are correctly classified. Determine the mean and variance of X. Round your answers to three decimal places (e.g. 98.765). Mean

Answer 1

Answer:
`\mu=2.88\ \&\ \sigma^2=0.115`

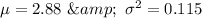
Explanation:

Given : The probability of a correct classification of any part is : p=0.96

sample size : n= 3

The formula to find the mean and variance for binomial distribution is given by :-

`\mu=np\\\\\sigma^2=np(1-p)`

Let the random variable X denote the number of parts that are correctly classified.

The, for the given situation, we have

`\mu=3(0.96)=2.88\\\\\sigma^2=(3)(0.96)(1-0.96)=0.1152\approx0.115`

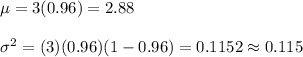
Hence, the mean and variance of X are 2.88 and 0.115 respectively.