Question

Suppose that on a dry, sunny day when the air temperature is near 37 ∘C,37 ∘C, a certain swimming pool would increase in temperature by 2.75 ∘C2.75 ∘C in one hour if not for evaporation. What fraction of the water in the pool must evaporate during this time to carry away precisely enough energy to keep the temperature of the pool constant?

Answer 1

The fraction of water body necessary to keep the temperature constant is 0,0051.

Step-by-step explanation:

Heat:

`Q=m*Ce*ΔT`

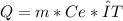
Q= heat (unknown)

m= mass (unknown)

Ce= especific heat (1 cal/g*°C)

ΔT= variation of temperature (2.75 °C)

Latent heat:

`ΔE=∝mΔHvap`

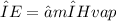
ΔE= latent heat

m= mass (unknown)

∝= mass fraction (unknown)

ΔHvap= enthalpy of vaporization (539.4 cal/g)

Since Q and E are equal, we can match both equations:

`m*Ce*ΔT=∝*m*ΔHvap`

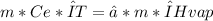
Mass fraction is:

`∝=(Ce*ΔT)/(ΔHvap)`

`∝=((1 cal/g*°C)*2.75°C)/(539.4 cal/g)`

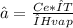
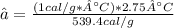
∝=0,0051