Question

The height of a ball above the ground as a function of time is given by the function h(t)=−32t2+8t+3 where h is the height of the ball in feet and t is the time in seconds. When is the ball at a maximum height? Round to 3 places past the decimal.

Answer 1

0.125 seconds.

Explanation:

We have been given that the height of a ball above the ground as a function of time is given by the function
`h(t)=-32t^2+8t+3`, where h is the height of the ball in feet and t is the time in seconds.

We can see that our given equation is a downward opening parabola as its leading coefficient is negative. The maximum point will be vertex of parabola.

To find the time, when the ball would be at its maximum height, we need to find the x-coordinate of vertex.

Using formula
`(-b)/(2a)`, we will find the x-coordinate of vertex of parabola as:

`(-b)/(2a)`

`(-8)/(2*-32)`

`(-8)/(-64)`

`(1)/(8)`

`0.125`

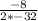
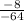
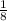
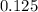
Therefore, the ball will be at a maximum height after 0.125 seconds.