Question

A rectangular garden of area 320 square feet is to be surrounded on three sides by a brick wall costing $ 10 per foot and on one side by a fence costing $ 6 per foot. Find the dimensions of the garden such that the cost of the materials is minimized.To minimize costs, the length of the side with a fence should be _____ feet and the length of the other side should be ____ feet.

Answer 1

To minimize costs, the length of the side with a fence should be 20 feet and the length of the other side should be 16 feet.

Explanation:

Let x and y be the sides of a rectangle. The area of a rectangle is
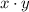`x\cdot y`. From the information given we know that the area is 320 square feet, so

`x\cdot y=320`

Now the quantity we want to optimize is going to be the cost to make our fence. We know that we have brick on three sides so we can say one side of length y and both sides of length x and the remanding side will be a fence. Thus we have the cost equation:

`C=10(y+2x)+6y=16y+20x`

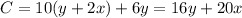
We can use the equation
`x\cdot y=320` to know the expression for x

`x=(320)/(y)`

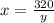
and put it into the cost equation to get the cost equation in terms of one variable:

`C=16y+20((320)/(y))\\C=16y+(6400)/(y)`

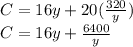
Next, we need to find the derivative of the cost equation and set it equal to zero

`(dC)/(dy)\left(16y+(6400)/(y)\right) = 16-(6400)/(y^2)`

`C'(y)=16-(6400)/(y^2)=0`

`16-(6400)/(y^2)=0\\16y^2-6400=0\\16y^2=6400\\y^2=(6400)/(16) \\y^2=400\\y=20`

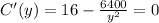
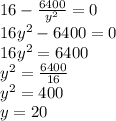
To check that this is indeed a value of y that gives us a minimum, we need to take the second derivative of our cost function

`C(y)''=(12800)/(y^3)`

`C(20)''=(12800)/(20^3)=1.6`

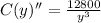
This value is greater than zero and we know that when the second derivative of a function is greater than zero the function has a minimum.

Now, we need values of both x and y, thus as

`y=20\\x=(320)/(y) =(320)/(20)=16`

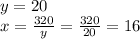
To minimize costs, the length of the side with a fence should be 20 feet and the length of the other side should be 16 feet.