Answer:
The probability that the average of the scores of all 400 students exceeds 19.0 is larger than the probability that a single student has a score exceeding 19.0
Explanation:
Xi~N(18.6, 6.0), n=400, Yi~Ber(p); Z~N(0, 1);

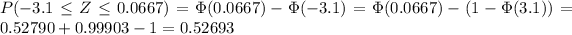
P(Xi≥19.0)=0.473
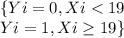
p=0.473
Yi~Ber(0.473)
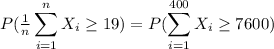
Based on the Central Limit Theorem:
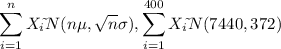
Then:
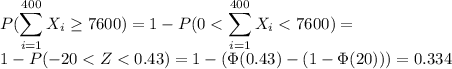
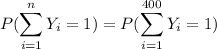
Based on the Central Limit Theorem:
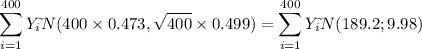

Then:
the probability that the average of the scores of all 400 students exceeds 19.0 is larger than the probability that a single student has a score exceeding 19.0