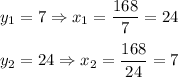Question

Un triángulo rectángulo tiene un área de 84 pies2 y una hipotenusa de 25 pies de largo. ¿Cuáles son las longitudes de sus otros dos lados?

Answer 1

7 feet and 24 feet

Explanation:

In the right triangle, the hypotenuse is 25 feet long. The area of this triangle is 84 square feet.

Let x feet and y feet be the lengths of triangle's legs.

By the Pythagorean theorem,

`x^2+y^2=25^2\\ \\x^2+y^2=625`

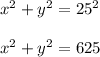
The area of the right triangle is half the product of its legs, thus

`84=(1)/(2)xy\\ \\xy=168`

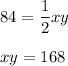
Solve the system of two equations:

`\left\{\begin{array}{l}x^2+y^2=625\\ \\xy=168\end{array}\right.`

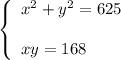
From the second equation:

`x=(168)/(y)`

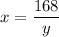
Substitute it into the first equation:

`\left((168)/(y)\right)^2+y^2=625\\ \\168^2+y^4=625y^2\\ \\y^4-625y^2+168^2=0\\ \\D=(-625)^2-4\cdot 168^2=(625-2\cdot 168)(625+2\cdot 168)=289\cdot 961=17^2\cdot 31\\ \\√(D)=17\cdot 31=527\\ \\y^2_(1,2)=(-(-625)\pm 527)/(2)=49,\ 576\\ \\y_1=7,\ y_2=-7,\ y_3=24,\ y_4=-24`

The length of the leg cannot be negative, so

`y_1=7\Rightarrow x_1=(168)/(7)=24\\ \\y_2=24\Rightarrow x_2=(168)/(24)=7`