Question

Chose parameters h and k such that the system has a) a unique solution, b) many solutions, and c) no solution. X1 + 3x2 = 4 2x1 + kx2 = h

Answer 1

a) k=1, h=1, the unique solution of the system is
`(x_1,x_2)=((1)/(5),(7)/(5))`

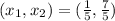
b) If k=6 and h=8 the system has infinite solutions.

c)If k=6 and h=3 the system has no solutions.

Explanation:

The augmented matrix of the system is
`\left[\begin{array}{ccc}1&3&4\\2&k&h\end{array}\right]`. If two times the row 1 is subtracted to row 2 we get the following matrix
`\left[\begin{array}{ccc}1&3&4\\0&k-6&h-8\end{array}\right]`.

Then

a) If k=1 and h=1, the unique solution of the system is
`x_2=(1-8)/(1-6)=(-7)/(-5)=(7)/(5)` and solviong for
`x_1`,

`x_1+3x_2=4\\\\x_1=4-3((7)/(5))=(1)/(5)`

Then the solution is
`(x_1,x_2)=((1)/(5),(7)/(5))`

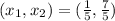
b) If k=6 and h=8 the system has infinite solutions because the echelon form of the matrix has a free variable.

c)If k=6 and h=3, the system has no solutions because the last equation of the system of the echelon form of the matrix is
`0x_2=-5`