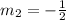Question

A segment has endpoints A(3, 4) and B(5, 8). What is the slope of the line parallel to the segment AB, and what is the slope of the line perpendicular to the segment AB?

Answer 1

Slope of a line perpendicular to the line AB =
`-(1)/(2)`

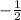
Slope of a line parallel to AB = 2

Explanation:

Let slope of a line =
`m_(1)`

And slope of the other line is =
`m_(2)`

If these lines are parallel then
`m_(1)=m_(2)`

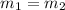
If these lines are perpendicular then
`m_(1)* m_(2)=-1`

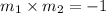
Slope of the line passing through two points (x, y) and (x', y') =
`(y-y')/(x-x')`

Therefore, slope of the line passing through A(3, 4) and B(5, 8) =
`(y-y')/(x-x')`

`m_(1)=(8-4)/(5-3)`

`m_(1)=2`

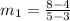
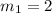
a). If a line having slope
`m_(2)` is parallel then
`m_(1)=m_(2)`

`m_(2)=2`

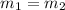
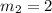
b). If a line having slope
`m_(2)` is perpendicular then
`2* m_(2)=-1`

`m_(2)=-(1)/(2)`

Answer 2

For this case we have that by definition, the slope of a line is given by:

`m = \frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}`

We have the following points:
`(x_ {1}, y_ {1}) :( 3,4)\\(x_ {2}, y_ {2}) :( 5,8)`

Substituting:

`m = \frac {8-4} {5-3} = \frac {4} {2} = 2`

By definition, if two lines are parallel then their slopes are equal. Thus, a line parallel to segment AB has slope
`m = 2`.

On the other hand, if two lines are perpendicular, then the product of their slopes is -1. So:

`m * 2 = -1\\m = - \frac {1} {2}`

Thus, a line perpendicular to segment AB has slope
`m = - \frac {1} {2}`

Answer:

a line parallel to segment AB has slope
`m = 2`.

a line perpendicular to segment AB has slope
`m = - \frac {1} {2}`