Question

How does the range of the pumpkin change if its initial velocity is tripled (keeping the angle fixed and less than 90∘)? How does the range of the pumpkin change if its initial velocity is tripled (keeping the angle fixed and less than )? The pumpkin's range is nine times as far. The pumpkin's range is eighteen times as far. The pumpkin's range is three times as far.

Answer 1

The pumpkin's range is nine times as far.

Step-by-step explanation:

Given,

In the first case,

Let a pumpkin is thrown with initial velocity u with an angel theta above the horizontal axis.

Therefore the range of the pumpkin is,

`R\ =\ (u^2sin2\theta)/(g)\,\,\,\,\,\,\,\,\,\,\,\,eqn(1)`

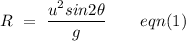
Now in the second case

Initial velocity of the pumpkin is three times the first case,

`\therefore U\ =\ 3u`

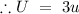
Let R' be the new range of the pumpkin.

New range of the pumpkin is,

`\therefore R'\ =\ (U^2sin2\theta)/(g)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,eqn(2)`

From eqn (1) and (2), we get,

`\therefore R'\ =\ ((3u)^2sin2\theta)/(g)\\\Rightarrow R'\ =\ (9u^2sin2\theta)/(g)\\\Rightarrow R'\ =\ 9 R`

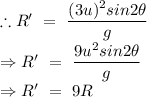
Hence the pumpkin's range is nine times of the initial case.