Question

Suppose that an insurance company classifies people into one of three classes — good risks, average risks, and bad risks. Their records indicate that the probabilities that good, average, and bad risk persons will be involved in an accident over a 1-year span are, respectively, .05, .15, and .30. If 20 percent of the population are "good risks," 50 percent are "average risks," and 30 percent are "bad risks," what proportion of people have accidents in a fixed year? If policy holder A had no accidents in 1987, what is the probability that he or she is a good (average) risk?

Answer 1

Answer: Our required probability is 0.745.

Explanation:

Since we have given that

Probability of getting good risks people = 0.05

Probability of getting average risks people = 0.15

Probability of getting bad risks people = 0.30

Probability of getting good risk accident = 0.2

Probability of getting average risk accident = 0.5

Probability of getting bad risk accident = 0.3

So, Probability of people having accident in a year is given by

`0.05* 0.2+0.15* 0.5+0.30* 0.3\\\\=0.175`

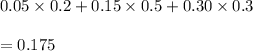
Probability of people either good or average risk given that he\she had no accident is given by

`=(0.2* 0.95+0.5* 0.85)/(1-0.175)\\\\=(0.615)/(0.825)\\\\=0.745`

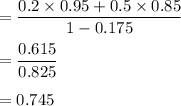
Hence, our required probability is 0.745.