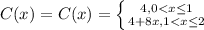Question

A taxi company charges $4.00 for the first mile (or part of a mile) and 80 cents for each succeeding tenth of a mile (or part). Express the cost C (in dollars) of a ride as a piecewise defined function of the distance x traveled (in miles) for 0 < x ≤ 2.

Answer 1

The piecewise function is:

`C(x) = C(x) = \left \{ {{4, 0< x \leq 1} \atop {4 + 8x, 1 < x \leq 2}}\right.`

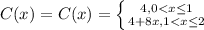
Explanation:

A piecewise function is a function that is defined in multiple intervals.

In the first interval:

`0 < x \leq 1`

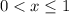
The problem states that a taxi company charges $4.00 for the first mile (or part of a mile).

x is the number of miles. So

If
`x \leq 1, C(x) = $4.00`.

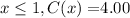Second interval:

`1 < x \ leq 2`

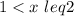
Here, the cost is defined by a linear function in the following format:

`C(x) = C_(0) + rx`

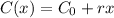
In which
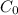`C_(0)` is the initial price and r is the price paid per mile.

The problem states that each succeeding tenth of a mile costs 80 cents. So

we have the following rule of three.

1 mile - r dollars

0.1miles - 0.8 dollars

`0.1r = 0.8`

`r = (0.8)/(0.1)`

`r = 8`

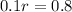
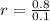
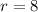
So, we have

`C(x) = 4 + 8x, 1 < x \leq 2`

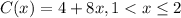
Piecewise function:

The piecewise function is:

`C(x) = C(x) = \left \{ {{4, 0< x \leq 1} \atop {4 + 8x, 1 < x \leq 2}}\right.`