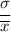Answer with explanation:
Given : A random sample of five Galaxy 8 smartphones is selected from the production line after final assembly, and the result of the weight control measurement is (in grams) are :
X= 155.1, 154.8, 155.5, 155.3, and 154.6.
here, n=5
The average weight :
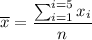
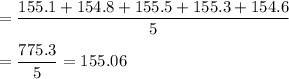
∴ Average weight (
 )=155.06 grams
)=155.06 grams
Uncertainty = Standard deviation:
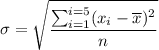
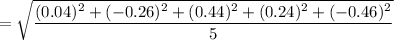
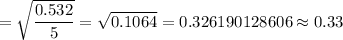
i.e. Its uncertainty :
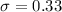
The fractional uncertainty =