Question

A suspension bridge is 60.0 m above the level base of a gorge. A stone is thrown or dropped from the bridge. Ignore air resistance. At the location of the bridge g has been measured to be 9.83 m/s2. (a) If you drop the stone, how long does it take for it to fall to the base of the gorge? (b) If you throw the stone straight down with a speed of 20.0 m/s, how long before it hits the ground? (c) If you throw the stone with a velocity of 20.0 m/s at 30.0° above the horizontal, how far from the point directly below the bridge will it hit the level ground?

Answer 1

a)
`t_(1)=3.49s`

b)
`t_(2)=2.00s`

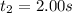
c)Xmax=80.71m

Step-by-step explanation:

a)Kinematics equation for the Stone, dropped:

`v(t)=v_(o)-g*t`

`y(t)=y_(o)+v_(o)t-1/2*g*t^(2)`

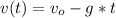
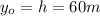`y_(o)=h=60m` initial position is bridge height

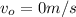`v_(o)=0m/s` the stone is dropped

The ball reaches the ground, y=0, at t=t1:

`0=h-1/2*g*t_(1)^(2)`

`t_(1)=√(2h/g)=√(2*60/9.83)=3.49s`

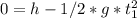
b)Kinematics equation for the Stone, with a initial speed of 20m/s:

`v(t)=v_(o)-g*t`

`y(t)=y_(o)+v_(o)t-1/2*g*t^(2)`

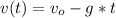
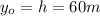`y_(o)=h=60m` initial position is bridge height

`v_(o)=-20m/s` the stone is thrown straight down

The ball reaches the ground, y=0, at t=t1:

`0=h+v_(o)t_(2)-1/2*g*t_(2)^(2)`

`0=60-20t_(2)-1/2*9.83*t_(2)^(2)`

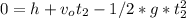
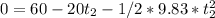
t2=-6.01 this solution does not have physical sense

t2=2.00

c)Kinematics equation for the Stone, with a initial speed of 20m/s with an angle of 30° above the horizontal:

`v(t)=v_(o)-g*t`

`y(t)=y_(o)+v_(o)t-1/2*g*t^(2)`

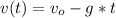
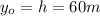`y_(o)=h=60m` initial position is bridge height

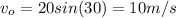`v_(o)=20sin(30)=10m/s` the stone is thrown with an angle of 30° above the horizontal

The ball reaches the ground, y=0, at t=t3:

`0=h+v_(o)t_(3)-1/2*g*t_(3)^(2)`

`0=60+10t_(3)-1/2*9.83*t_(3)^(2)`

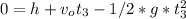
t3=-2.62 this solution does not have physical sense

t3=4.66

the movement in x:

v=constant=20cos(30)m/s

x(t)=v*t

Xmax=v*t3=20cos(30)*4.66=80.71m