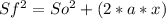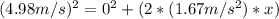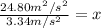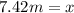Answer:
The speed in the first point is: 4.98m/s
The acceleration is: 1.67m/s^2
The prior distance from the first point is: 7.42m
Step-by-step explanation:
For part a and b:
We have a system with two equations and two variables.
We have these data:
X = distance = 60m
t = time = 6.0s
Sf = Final speed = 15m/s
And We need to find:
So = Inicial speed
a = aceleration
We are going to use these equation:
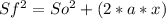
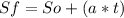
We are going to put our data:
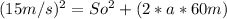
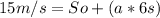
With these equation, you can decide a method for solve. In this case, We are going to use an egualiazation method.
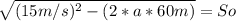
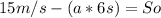
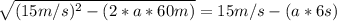
![[√((15m/s)^2-(2*a*60m))]^(2)=[15m/s-(a*6s)]^(2)](https://img.qammunity.org/2020/formulas/physics/high-school/qn8qau27te66qwzo4f3ku28jjdpxyiiupd.png)

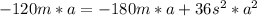


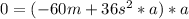
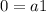
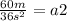

If we analyze the situation, we need to have an aceleretarion greater than cero. We are going to choose a = 1.67m/s^2
After, we are going to determine the speed in the first point:
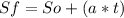

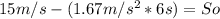
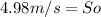
For part c:
We are going to use: