Answer:
For 11. x = 15 and y = 15 ; ∠GFQ = 45°
Explanation:
Work for 11.
Know that when you add ∠GFS ∠QFP ∠PFT to ∠GFQ it should equal 180° because they are supplementary.
(2x + y) + (3x) + (3x + y) + (x + y) = 180
(5x + y) + (4x + 2y) = 180
9x + 3y = 180
Then add ∠GFQ ∠QFP ∠PFT ∠TFE
(3x) + (3x + y) + (x + y) + (3x) = 180
(6x + y) + (4x + y) = 180
10x + 2y = 180
Make the 2 equations equal to each other to find x and y.
9x + 3y = 10x + 2y
- 9x - 9x
3y = x + 2y
- 2y - 2y
y = x
Then plug in for y for ∠QFP ∠PFT
(3x + (x)) + (x + (x)) = 90
4x + 2x = 90
6x = 90
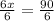
x = 15
Then plug in x for ∠GFQ
3(15) = 45
Then to find y you add ∠GFQ and ∠QFS and plug in for x.
45 + (2(15) + y) = 90
45 + 30 + y = 90
75 + y = 90
- 75 - 75
y = 15