Question

In the following ordinary annuity, the interest is compounded with each payment, and the payment is made at the end of the compounding period. Find the amount of time needed for the sinking fund to reach the given accumulated amount. (Round your answer to two decimal places.) $255 monthly at 5.8% to accumulate $25,000.

Answer 1

Ans. the amount of time needed for the sinking fund to reach $25,000 if invested $255/month at 5.8% compounded monthly (Effective monthly=0.4833%) is 80.45 months.

Explanation:

Hi, first we need to transform that 5.8% compounded monthly into an effective monthly rate, that is as follows.

`r(EffectiveMonthly)=(r(Comp.Monthly))/(12) =(0.058)/(12) =0.00483`

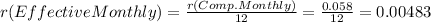
That means that our effective monthly rate is 0.483%

Now, we need to solve for "n" the following formula.

`FutureValue=(A((1+r)^(n)-1) )/(r)`

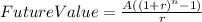
Let´s start solving

`25,000=(255((1.00483)^(n)-1) )/(0.00483)`

`(25,000*0.00483)/(255) =1.00483^(n) -1\\`

`0.47352941=1.00483^(n) -1`

`1+0.47352941=1.00483^{n`

`1.47352941=1.00483^(n)`

`Ln(1.47352941)=n*Ln(1.00483)`

`(Ln(1.47352941))/(Ln(1.00483)) =n=80.45`

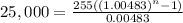
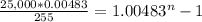
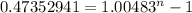
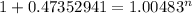
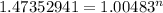
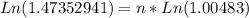
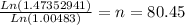
This means that it will take 80.45 months to reach $25,000 with an annuity of $255 at a rate of 5.8% compounded monthly (0.4833% effective monthly).

Best of luck.