Answer with Step-by-step explanation:
We are given that twos sets
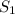 ={a+bx:
={a+bx:
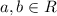 }=All polynomials which can expressed as a linear combination of 1 and x.
}=All polynomials which can expressed as a linear combination of 1 and x.
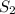 ={ax+b(2+x):
={ax+b(2+x):
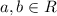 }=All polynomials which can be expressed as a linear combination of x and 2+x.
}=All polynomials which can be expressed as a linear combination of x and 2+x.
We have to prove that given two sets are same.
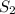 ={ax+2b+bx}={(a+b)x+2b}={cx+d}
={ax+2b+bx}={(a+b)x+2b}={cx+d}
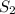 ={cx+d}=All polynomials which can be expressed as a linear combination of 1 and x.
={cx+d}=All polynomials which can be expressed as a linear combination of 1 and x.
Because a+b=c=Constant
2b= Constant=d
Hence, the two sets are same .