Question

Charge g is distributed in a spherically symmetric ball of radius a. (a) Evaluate the average volume charge density p. (b) Now assume p(r) is directly proportional to r. (i) Derive the formula for p(r) in terms of r, Q, and a. At what value of r does p(r)= ? [Ans: 340] (ii) Find q(r), and graph it.

Answer 1

Step-by-step explanation:

The volume of a sphere is:

V = 4/3 * π * a^3

The volume charge density would then be:

p = Q/V

p = 3*Q/(4 * π * a^3)

If the charge density depends on the radius:

p = f(r) = k * r

I integrate the charge density in spherical coordinates. The charge density integrated in the whole volume is equal to total charge.

`Q = \int\limits^(2*\pi)_0\int\limits^\pi_0  \int\limits^r_0 {k * r} \, dr * r*d\theta* r*d\phi`

`Q = k *\int\limits^(2*\pi)_0\int\limits^\pi_0  \int\limits^r_0 {r^3} \, dr * d\theta* d\phi`

`Q = k *\int\limits^(2*\pi)_0\int\limits^\pi_0 {(r^4)/(4)} \, d\theta* d\phi`

`Q = k *\int\limits^(2*\pi)_0 {(\pi r^4)/(4)} \,  d\phi`

`Q = (\pi^2 r^4)/(2)}`

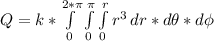
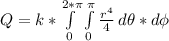
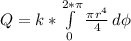
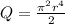
Since p = k*r

Q = p*π^2*r^3 / 2

Then:

p(r) = 2*Q / (π^2*r^3)