Question

If a body travels half it’s total path in the last 1.10s if it’s fall from rest, find the total time of its fall (in seconds)

Answer 1

3.75s

Step-by-step explanation:

We can use the equations for constant acceleration motion. Let's call x, the total length of the path, then x/2 will be half of path. After falling from rest and reaching the half of its total path, the velocity of the body will be:

`v_f^2 =v_0^2 + 2a(x/2)`

vf is the final velocity, v0 is the initial velocity, 0m/s because the body starts from rest. a is the acceleration, gravity = 9.81m/s^2 in this case. Now, clearing vf we get:

`v_f=√((0m/s)^2 + 2g(x/2))\\v_f = √(g*x)</p><p></p><p>In the second half:</p><p>[tex]x/2 = (1)/(2)gtx^(2)  + v_ot`

`x/2 = (1)/(2)g*(t)^2 + √(g*x)*(t)`

`((1)/(2)((x-gt^2))/(√(g)t))^2 = x\\\\(1)/(4gt^2)(x^2 - 2xgt^2 + g^2t^4) = x\\\\(1)/(4gt^2)x^2 - ((2gt^2)/(4gt^2)+1)x + (g^2t^4)/(4gt^2) = 0\\ (1)/(4gt^2)x^2 - (3)/(2)x + (gt^2)/(4) = 0\\`

`0.0211 x^2 - 1.5x + 2.97 = 0\\`

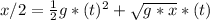
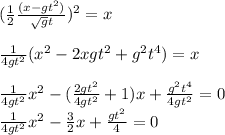
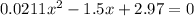
Solving for x, you get that x is equal to 69.2 m or 2.03m. The total time of the fall would be:

`x = (1)/(2)gt^2\\t=√((2x/g))`

Trying both possible values of x:

`t_1 = 3.75 s\\t_2 = 0.64 s`

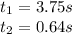
t2 is lower than 1.1s, therefore is not a real solution.

Therefore, the path traveled will be 69.2m and the total time 3.75s