Question

A rigid adiabatic container is divided into two parts containing n1 and n2 mole of ideal gases respectively, by a movable and thermally conducting wall. Their pressure and volume are P1, V1 for part 1 and P2, V2 for part 2 respectively. Find the final pressure P and temperature T after the two gas reaches equilibrium. Assume the constant volume specific heats of the two gas are the same.

Answer 1

Step-by-step explanation:

Given

Pressure, Temperature, Volume of gases is

`P_1, V_1, T_1 & P_2, V_2, T_2`

Let P & T be the final Pressure and Temperature

as it is rigid adiabatic container therefore Q=0 as heat loss by one gas is equal to heat gain by another gas

`-Q=W+U_1----1`

`Q=-W+U_2-----2`

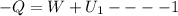
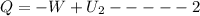
where Q=heat loss or gain (- heat loss,+heat gain)

W=work done by gas

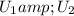`U_1 & U_2` change in internal Energy of gas

Thus from 1 & 2 we can say that

`U_1+U_2=0`

`n_1c_v(T-T_1)+n_2c_v(T-T_2)=0`

`T(n_1+n_2)=n_1T_1+n_2T_2`

`T=(n_1+T_1+n_2T_2)/(n_1+n_2)`

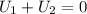
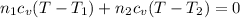
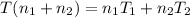
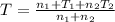
where
`n_1=(P_1V_1)/(RT_1)`

`n_2=(P_2V_2)/(RT_2)`

`T=((P_1V_1)/(RT_1)* T_1+(P_2V_2)/(RT_2)* T_2)/((P_1V_1)/(RT_1)+(P_2V_2)/(RT_2))`

`T=(P_1V_1+P_2V_2)/((P_1V_1)/(T_1)+(P_2V_2)/(T_2))`

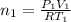
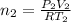
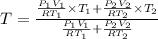
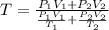
and
`P=(P_1V_1+P_2V_2)/(V_1+V_2)`