Question

Proof by Contradiction : Show that √ 2 is irrational.

Answer 1

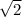`\sqrt2` is irrational

Step-by-step explanation:

Let us assume that
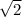`\sqrt2` is rational. Thus, it can be expressed in the form of fraction
`(x)/(y)`, where x and y are co-prime to each other.

`\sqrt2` =
`(x)/(y)`

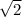Squaring both sides,

`2 = (x^2)/(y^2)`

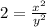
Now, it is clear that x is an even number. So, let us substitute x = 2u

Thus,

`2 = ((2u)^2)/(y^2)\\y^2 = 2u^2`

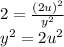
Thus,
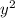`y^2`is even, which follows the fact that y is also an even number. But this is a contradiction as x and y have a common factor that is 2 but we assumed that the fraction
`(x)/(y)` was in lowest form.

Hence,
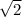`\sqrt2` is not a rational number. But
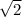`\sqrt2` is a an irrational number.