Question

Light of wavelength 597 nm falls on a double slit, and the first bright fringe of the interference pattern is seen at an angle of 15.8° with the horizontal. Find the separation between the slits. µm

Answer 1

The separation between the slit is
`2.19\mu m`

Solution:

As per the question:

Wavelength of light,
`\lambda = 597 nm = 597* 10^(-9) m`

`\theta = 15.8^(\circ)`

Now, by Young's double slit experiment:

`xsin\theta = n\lambda`

here,

n = 1

x = slit width

Therefore,

`x = (597* 10^(-9))/(sin15.8^(\circ)) = 2.19* 10^(- 6) m`

`x = 2.19\mu m`

Answer 2

2.2 µm

Step-by-step explanation:

For constructive interference, the expression is:

`d* sin\theta=m* \lambda`

Where, m = 1, 2, .....

d is the distance between the slits.

Given wavelength = 597 nm

Angle,
`\theta` = 15.8°

First bright fringe means , m = 1

So,

`d* sin\ 15.8^0=1* \597\ nm`

`d* 0.2723=1* \597\ nm`

`d=2192.43481\ nm`

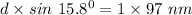
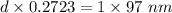
Also,

1 nm = 10⁻⁹ m

1 µm = 10⁻⁶ m

So,

1 nm = 10⁻³ nm

Thus,

Distance between slits ≅ 2.2 µm