Question

Find the Cartesian Equation of the plane passing through P(8, -2,0) and perpendicular to a- 5i+3j-k What is the distance of this plane to the point 0(2,2, 2)? (a) (b)

Answer 1

equation of plane, 5x+3y-z-36=0

Distance of point (2,2,2) from plane = 4.05 units

Explanation:

Given,

Plane passing through the point = (8, -2, 0)

Let's say,
`x_1\ =\ 8`

`y_1\ =\ -2`

`z_1\ =\ 0`

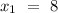
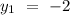
Plane perpendicular to the vector, a= 5i + 3j- k

Since, the vector is perpendicular to the plane, hence the equation of plane can be given by

`(5i + 3j- k).((x-x_1)i+(y-y_1)j+(z- z_1)k)=\ 0`

`=>(5i + 3j- k).((x-8)i+(y+2)j+(z-0)k)=\ 0`

`=>\ 5(x-8)+3(y+2)-z=0`

`=>\ 5x\ -\ 40\ +\ 3y\ +\ 6\ -\ z\ =\ 0`

`=>\ 5x\ +\ 3y\ -\ z\ -\ 36\ =\ 0`

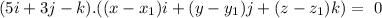
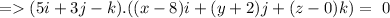
Hence, the equation of plane can be given by, 5x+3y-z-36=0

Now, we have to calculate the distance of the point O(2,2,2) from the plane 5x+3y-z-36=0

Let's say,

a= 5, b= 3, c= -1, d=-36

`x_0=2,\ y_0=2,\ z_0=2`

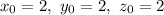
So, distance of a point from the plane can be given by,

`d=(ax_0+by_0+cz_0+d)/(√(a^2+b^2+c^2))`

`=(\left |5* 2+3* 2+(-1)* 2-36\right |)/(√(5^2+3^2+(-1)^2))`

`=(24)/(√(35))`

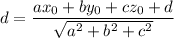
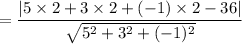
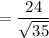
= 4.05 units

So, the distance of the point O(2,2,2) from the given plane will be 4.05 units.