Question

If you mix 50mL of 0.1 M TRIS acid with 60 mL of0.2 M

TRIS base, what will be the resulting pH?

Answer 1

Answer: The pH of resulting solution is 8.7

Step-by-step explanation:

To calculate the number of moles for given molarity, we use the equation:

`\text{Molarity of the solution}=\frac{\text{Moles of solute}* 1000}{\text{Volume of solution (in mL)}}`

• For TRIS acid:

Molarity of TRIS acid solution = 0.1 M

Volume of solution = 50 mL

Putting values in above equation, we get:

`0.1M=\frac{\text{Moles of TRIS acid}* 1000}{50mL}\\\\\text{Moles of TRIS acid}=0.005mol`

• For TRIS base:

Molarity of TRIS base solution = 0.2 M

Volume of solution = 60 mL

Putting values in above equation, we get:

`0.2M=\frac{\text{Moles of TRIS base}* 1000}{60mL}\\\\\text{Moles of TRIS base}=0.012mol`

Volume of solution = 50 + 60 = 110 mL = 0.11 L (Conversion factor: 1 L = 1000 mL)

• To calculate the pH of acidic buffer, we use the equation given by Henderson Hasselbalch:

`pH=pK_a+\log(([salt])/([acid]))`

`pH=pK_a+\log(\frac{[\text{TRIS base}]}{[\text{TRIS acid}]})`

We are given:

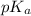`pK_a` = negative logarithm of acid dissociation constant of TRIS acid = 8.3

`[\text{TRIS acid}]=(0.005)/(0.11)`

`[\text{TRIS base}]=(0.012)/(0.11)`

pH = ?

Putting values in above equation, we get:

`pH=8.3+\log((0.012/0.11)/(0.005/0.11))\\\\pH=8.7`

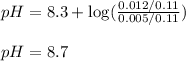
Hence, the pH of resulting solution is 8.7