Question

Find the most general antiderivative of the function. (Check yo f(x) = 3^x + 7 sinh(x) F(x) = Need Help? Watch It Talk to a Tutor

Answer 1

F(x)=
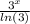`(3^x)/(ln(3))`+7cosh(x)+C

Step-by-step explanation:

The function is f(x)=3ˣ+7sinh(x), so we can define it as f(x)=g(x)+h(x) where g(x)=3ˣ and h(x)=7sinh(x).

Now we have to find the most general antiderivative of the function this means that we have to calculate
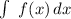`\int\ {f(x)} \, dx` wich is the same as
`\int\ {(g+h)(x)} \, dx`

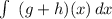
The sum rule in integration states that the integral of a sum of two functions is equal to the sum of their integrals. Then,

`\int\ {(g+h)(x)} \, dx` =
`\int\ {g(x)} \, dx + \int\ {h(x)} \, dx`

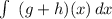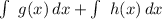
1-
`\int\ {g(x)} \, dx =`
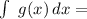
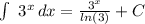`\int\ {3^x} \, dx = (3^x)/(ln(3))+C` this is because of the rule for integration of exponencial functions, this rule is:

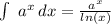`\int\ {a^x} \, dx =(a^x)/(ln(x))`, in this case a=3

2-
`\int\ {h(x)} \, dx =`
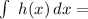
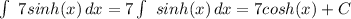`\int\ {7sinh(x)} \, dx =7\int\ {sinh(x)} \, dx =7cosh(x)+C` , number seven is a constant (it doesn´t depend of "x") so it "gets out" of the integral.

The result then is:

F(x)=
`\int\ {(h+g)(x)} \, dx=\int\ {h(x)} \, dx +\int\ {g(x)} \, dx`

`\int\ {3^x} \, dx +\int\ {7sinh(x)} \, dx = (3^x)/(ln(3)) +7cosh(x) + C`

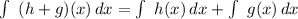
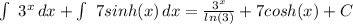
The letter C is added because the integrations is undefined.