Question

Consider strings of length 10 which contain only letters from the set {A, E, I, O, U} and digits from {1, 3, 5, 7, 9}. Suppose repitition of letters is not allowed.

How many different strings are there?
How many different strings are there if the letters, i.e. A, E, I, O, U and the digits, i.e. 1,3, 5, 7, 9 must alternate?
How many different strings are there if all five letters must be adjacent in each string?

Answer 1

a) There are 3,628,800 different strings.

b) There are 28,800 different strings if the letters ad digits must alternate.

c)There are 86,400 different string if all five letters must be adjacent in each string.

Explanation:

There are 10 digits.

Our strings have the following format:

C1 - C2 - C3 - C4 - C5 - C6 - C7 - C8 - C9 - C10

repitition of letters is not allowed.

a) How many different strings are there?

C1 can be any of the 10, C2 can be 9, C3 can be 8, ...

So in total there are:

`T = 10*9*8*7*6*5*4*3*2*1 = 3,628,800`

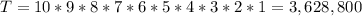
There are 3,628,800 different strings.

b) How many different strings are there if the letters, i.e. A, E, I, O, U and the digits, i.e. 1,3, 5, 7, 9 must alternate?

There are the following possiblities:

5(l) - 5(d) - 4(l) - (4d) - ...

Or

5(d) - 5(l) - 4(d) - 4(l) - ...

So:

`T = 2*(5*5*4*4*3*3*2*2*1*1) = 28,800`

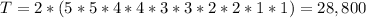
There are 28,800 different strings if the letters ad digits must alternate.

c) How many different strings are there if all five letters must be adjacent in each string?

L - L - L - L - L - D - D - D - D - D

D - L - L - L - L - L - D - D - D - D

D - D - L - L - L - L - L - D - D - D

D - D - D - L - L - L - L - L - D - D

D - D - D - D - L - L - L - L - L - D

D - D - D - D - D - L - L - L - L - L

There are
`T = 6*(5*5*4*4*3*3*2*2*1*1) = 86,400`

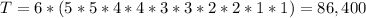
There are 86,400 different string if all five letters must be adjacent in each string.