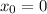Question

D) Find the 5th degree Taylor polynomial centered at x = 0 for the function y = \tiny \frac{x}{1+x}

Answer 1

`P(x) = x - x^2 + x^3 - x^4+x^5`

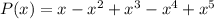
Explanation:

Let us first remember how a Taylor polynomial looks like:

Given a differentiable function
`f` then we can find its Taylor series to the
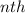`nth` degree as follows:

`P(x) = f(x_(0)) + f'(x_(0)).(x-x_(0)) + (f''(x_(0)))/(2!).(x-x_(0))^2+.....+(f^n(x_(0)))/(n!).(x-x_(0))^n + R_(n)(x).(x-x_(0))^n`

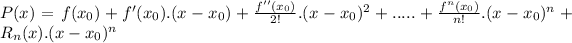
Where
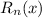`R_(n)(x)` represents the Remainder and
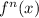`f^n(x)` is the
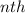`nth` derivative of
`f`.

So let us find those derivatives.

`f(x) = (x)/(1+x)\\f'(x) = (1)/((1+x)^2)\\f''(x) = (-2)/((1+x)^3)\\f'''(x) = (6)/((1+x)^4)\\f''''(x) = (-24)/((1+x)^5)\\f'''''(x) = (120)/((1+x)^6)`

The only trick for this derivatives is for the very first one:

`f'(x) = (1)/(1+x) - (x)/((1+x)^2)\\f'(x) = ((1+x) - x)/((1+x)^2) = (1)/((1+x)^2)\\`

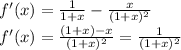
Then it's only matter of replacing on the Taylor Series and replacing
`x_(0)=0`