Question

Prove the following statement using a proof by contraposition. Yr EQ,s ER, if s is irrational, then r + 1 is irrational.

Answer 1

I think that what you are trying to show is: If
`s` is irrational and
`r` is rational, then
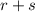`r+s` is rational. If so, a proof can be as follows:

Explanation:

Suppose that
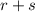`r+s` is a rational number. Then
`r` and
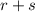`r+s` can be written as follows

`r=(p_(1))/(q_(1)), \,p_(1)\in \mathbb{Z}, q_(1)\in \mathbb{Z}, q_(1)\\eq 0`

`r+s=(p_(2))/(q_(2)), \,p_(2)\in \mathbb{Z}, q_(2)\in \mathbb{Z}, q_(2)\\eq 0`

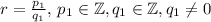
Hence we have that

`r+s=(p_(1))/(q_(1))+s=(p_(2))/(q_(2))`

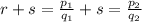
Then

`s=(p_(2))/(q_(2))-(p_(1))/(q_(1))=(p_(2)q_(1)-p_(1)q_(2))/(q_(1)q_(2))\in \mathbb{Q}`

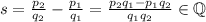
This is a contradiction because we assumed that
`s` is an irrational number.

Then
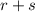`r+s` must be an irrational number.