Answer: The proof is done below.
Step-by-step explanation: Given that A is a 3 x 3 matrix such that det (A) = 9.
We are to prove the following :

For a non-singular matrix B of order n, we have two two properties of its determinant :
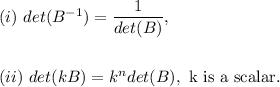
Therefore, we get
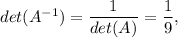
and so,
![det(3A^(-1))~~~~~~~[\textup{since A is of order 3}]\\\\=3^3det(A^(-1))\\\\=27*(1)/(9)\\\\=3.](https://img.qammunity.org/2020/formulas/mathematics/college/pmza5p1x65h1krmpverwvqvy0a75hlu0zt.png)
Hence proved.