Question

Consider the quadratic function f(x) = -x^2 + 1x + 12. Determine the following: (enter all numerical answers as integers, fractions, or decimals): The smallest -intercept is 2 = The largest x-intercept is z = The y-intercept is y = The vertex is ( The line of symmetry has the equation Preview

Answer 1

Answer and Explanation:

Given : The quadratic function
`f(x)=-x^2+x+12`

To find : Determine the following ?

Solution :

The x -intercept are where f(x)=0,

So,
`-x^2+x+12=0`

Applying middle term split,

`-x^2+4x-3x+12=0`

`-x(x-4)-3(x-4)=0`

`(x-4)(-x-3)=0`

`x=4,-3`

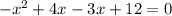
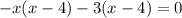
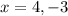
The x-intercepts are (4,0) and (-3,0).

The smallest x-intercept is x=-3

The largest x-intercept is x=4

The y -intercept are where x=0,

So,
`f(0)=-(0)^2+0+12`

`f(0)=12`

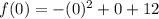
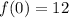
The y-intercept is y=12.

The quadratic function is in the form,
`y=ax^2+bx+c`

On comparing, a=-1 , b=1 and c=1 2

The vertex of the graph is denote by (h,k) and the formula to find the vertex is

For h, The x-coordinate of the vertex is given by,

`h=-(b)/(2a)`

`h=-(1)/(2(-1))`

`h=(1)/(2)`

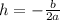
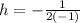
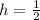
For k, The y-coordinate of the vertex is given by,

`k=f(h)`

`k=-h^2+h+12`

`k=-((1)/(2))^2+(1)/(2)+12`

`k=-(1)/(4)+(1)/(2)+12`

`k=(-1+2+48)/(4)`

`k=(49)/(4)`

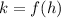
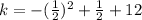
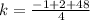
The vertex of the function is
`(h,k)=((1)/(2),(49)/(4))`

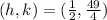
The x-coordinate of the vertex i.e.
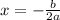`x=-(b)/(2a)` is the axis of symmetry,

So,
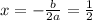`x=-(b)/(2a)=(1)/(2)` (solved above)

The axis of symmetry is
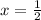`x=(1)/(2)`.