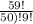Question

An exam has 10 problems. How many ways can (integer points be assigned to the problems if the total of the points is 100 and each problem is worth at least 5 points?

Answer 1

number of way is
`(59!)/(50)!9!)`

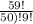
Explanation:

given data:

total number of problems 100

total points for each problem 5

let ten problems are

`x_1, x_2,........., x_(10)`

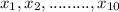
according to the given information

`x_1 +x_2 +.......+x_(10) = 100`

`x_i \geq 5`

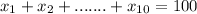
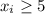
where i =1 + 10

so, number of way integer point can assign are

`^((n+r-1))C_((r-1))`

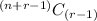
where

r = 10

`n = 100 - 10* 5 = 50`

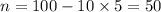
so, we have

`^((59))C_(9)`

`(59!)/(59-9)!9!)`

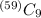
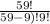
number of way is
`(59!)/(50)!9!)`