Question

There are 14 juniors and 16 seniors in a chess club. a) From the 30 members, how many ways are there to arrange 5 members of the club in a line? b) How many ways are there to arrange 5 members of the club in a line if there must be a senior at the beginning of the line and at the end of the line? 0 c) If the club sends 2 juniors and 2 seniors to the tournament, how many possible groupings are there? d) If the club sends either 4 juniors or 4 seniors, how many possible groupings are there?

Answer 1

No. of juniors = 14

No. of seniors = 16

Total students = 30

A) From the 30 members, how many ways are there to arrange 5 members of the club in a line?

Since we are asked about arrangement so we will use permutation

Formula :
`^nP_r=(n!)/((n-r)!)`

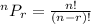
n = 30

r = 5

`^(30)P_5=(30!)/((30-5)!)`

`^(30)P_5=17100720`

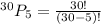
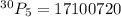
So, From the 30 members, there are 17100720 ways to arrange 5 members of the club in a line?

B) How many ways are there to arrange 5 members of the club in a line if there must be a senior at the beginning of the line and at the end of the line?

Out of 16 seniors 2 will be selected

So, 3 places are vacant

Remaining students = 30-2 = 28

So, out of 28 students 3 students will be selected

No. of ways =
`^(16)P_2 * ^(28)P_3`

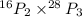
No. of ways =
`(16!)/((16-2)!)*(28!)/((28-3)!)`

=
`4717440`

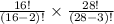
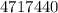
There are 4717440 ways to arrange 5 members of the club in a line if there must be a senior at the beginning of the line and at the end of the line.

C)If the club sends 2 juniors and 2 seniors to the tournament, how many possible groupings are there?

Since we are not asked about arrangement so we will use combination

Out of 16 seniors 2 will be selected

Out of 14 juniors 2 will be selected

Formula :
`^nC_r=(n!)/(r!(n-r)!)`

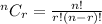
So, No. of possible groupings =
`^(16)C_2 * ^(14)C_2`

=
`(16!)/(2!(16-2)!) * (14!)/(2!(14-2)!)`

=
`10920`

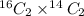
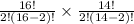
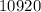
If the club sends 2 juniors and 2 seniors to the tournament, there are 10920 possible groupings

D) If the club sends either 4 juniors or 4 seniors, how many possible groupings are there?

Out of 16 seniors 4 will be selected

or

Out of 14 juniors 4 will be selected

So, No. of possible groupings =
`^(16)C_4 + ^(14)C_4`

=
`(16!)/(4!(16-4)!) + (14!)/(4!(14-4)!)`

=
`2821`

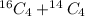
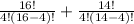
So,If the club sends either 4 juniors or 4 seniors, there are 2821 possible groupings .